这里说的成绩估计预测是指对整体（整个班级）的预测，不是对某个学生的成绩预测。
如果要预测某个单独的学生将比这复杂，包括心理的、智力的、本人往年的成绩、全市往年的成绩数据、家庭的等等，这既是教学的，也是心理咨询的部分，留待以后整理。
在预测前先了解几个概念。
一、总体、样本
总体：就是想了解的全部，在这里就是即将预测的整体。比如想了解全区全市的六年级科学考试成绩。
平时因为各种原因，是没有办法了解全市的成绩的，上级领导也不可能告诉您！这涉及到多方面因素。
样本：整体里的一部分，也就是得到的数据，在这里就是您手上的您们班或您教年级的学生成绩。
整体---样本，其实在统计里还有很严格的定义，先不管定义了，大概就这样理解不会太错。
这时候您又想知道，比如，自己教的如何？自己学生水平如何？——该怎么办？
平时，您也不想到了真正比分数、比成绩的时候才知道自己挨了！
不要误解阳光教育，阳光教育不是把成绩放阳光下，让你随点乱点一下就能得到成绩的。
您手上又只有自己所交班级或年级的成绩，是不是有点办法？
大概是有点办法的，往下看即可。
统计里的样本比这里的样本要自由的多，是可以随便抽取的，但是成绩可没有这自由——如果真的可以选了这个学生，又选那个学生，根本就不用预测，直接把每个学生都问一遍登记分数，算一算就可以了——虽然有几万或几十万，但是对现在来说工作量其实也不大——1分钟5个，1小时300个，1天7200个，1月216000个——这也不现实，就是996，也不能只登记分数！——早被通报了。
反正，您想知道全部成绩的大概，就的想另外的办法。
二、均分
把每个人的分数加起来除以班上总人数就是均分。
均分=（学生1分数+学生2分数……+学生n分数）/学生人数n
三、标准差
我们平时看一个班的成绩，多是看平均分，也就是大家平均考好多。
但是，大家都知道两极分化——好的好，差的差——万一好的就几个，尾巴一大片，那就恼火了。
这种班级教起来很费神，因为差的可能越来越差，好的也被拖跨——重新分班？好想法！谁敢？还是认识一下马岱吧。
这就得想办法采取折中教法。快的慢点，慢的多点。快的少花点时间讲，慢得多花点时间讲，比如课后辅导等等。
嗯！怎么衡量差距？
与平均分比较！
也就是每个人的成绩与班上的均分的差距。
班上均分只有一个，差距有n个，有多少学生，就有多少个差距。以谁的为准来衡量呢？以谁的为准都是歧视！
不如把大家的加起来再平均，这样就能照顾到大家了。
比均分高的，就是正数，比均分低的就是负数，不太好处理。——把每个都平方，就都是正数了。
把每一个这样的到的数值全部加起来，就得到一个平方数。
距离和的分数=（学生1的分数-均分）²+（学生2的分数-均分）²……+（学生n的分数-均分）²
但这是平方，均分可没平方，再开方，量纲就一样了。
这就是标准差。
衡量的是每个人与均分的差距，也就是离均分有多远。
标准差就是一种度量，就像温度是一种度量一样，只是温度可以用温度计来实物化后度量，而标准差无法实物化，因为他每次会因为要统计的数量的个数多少而变化，所以生活中难以找到一个形象的比喻理解，比较抽象。
可以把标准差想象成量纲，是一种度量，参数估计、假设检验都用这个量纲来衡量及选取。

下面是数据分析给出的数据，对比这两张图是说，不用手工计算，关键是知道怎么回事。

附：
各软件计算的结果是一样的，只是精度稍有差别。

四、置信区间
信——信心。
置——放置。
区间——范围。
合起来就是把信心放在范围里。
置信区间就是把握的范围、程度意思。
平时，大家都会说，我有百分之百的把握他是抄的。（这关系到另一话题——游程检验考试是否有抄袭）。
这也太绝对了——不太好。
百分之八九十就可以了——八九不离十，万一有点意外也是正常的。错了这次还有下次，错了今生还有来世——不要有执念。
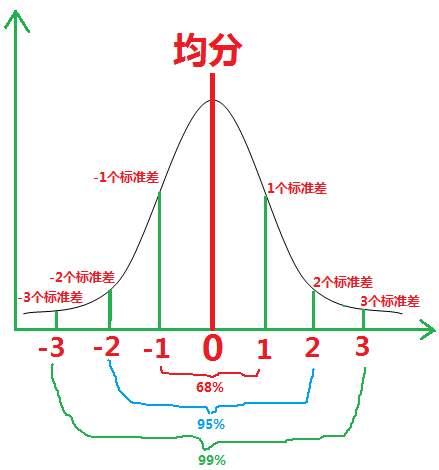
统计上常用的三个把握：68%、95%、99%。
记住这三个，后面还要用。
五、置信区间包括多少人
（一）置信区间和标准差
为了预测成绩，当然需要一定的把握，也需要一定的区间，二者要平衡。
不可能说，有百分百的把握在0-100分之间，这就是屁话，没有用处。
那么，置信区间怎么选取呢？当然，像上面提到的，八九不离十，是可以的。是不是就选百分之八九十的学生，对这些写生有没有要求？排不排序？随便乱挑？为什么选百分之八九十？百分之八九十是怎么确定的？
在选取的时候，会结合上面的标准差来选取。也就是按距离远近来选取。
既然标准差就是量纲单位，那么，我们按不同单位来选取。
怎样才能比较有把握？统计学家早就计算出来了，我们只需要运用就可以了。
等等！有点不信？我也是！
我们先看看吧！
（二）标准差和置信区间包括的人数
1.一个标准差有多少人？

看实例：
标准差为13.808，我们把比均高13.808的人和比均分低13.808的人挑出来，看有多少学生？
均分=73.69
也就是选取：
低分数为：73.69-13.808=59.806679-->60分
高分数为：73.69+13.808=87.423321-->88分
在[60,88]分数范围的人我们就挑出来，看有多少人。


246/325=75.69%
咦！有点不对！统计书上的数据可有点不一样！
嗯！可能是数据量的问题。下面模拟一下统计操作。
因为数据在数据库里，前面的的操作就先不管了。
大概步骤是连接数据库，然后随机抽60个学生，算出均分，这样反复抽540000次，得到540000个均值，把这些均值看成（模拟成）540000个学生，然后算出均分。
t<-540000
c<-replicate(t,mean(sample(b,size=60,replace = T)))
write.csv(c,file = "C:\\Users\\Administrator\\Desktop\\bc.csv",row.names = F)

1个西格玛内的数据是：
[71.910268,75.464952]有368415个，占68.225%
这就接近统计学书上的数据了。

从这幅图大概可以看出各个分数的个数（频率）。
因为统计是有关大量数据（大数据）的科学，在这里因为数据量的问题，并不能否定统计的原理。
2.两个标准差有多少人？

看实例：
标准差为13.808，我们把比均高两个13.808的人和比均分低两个13.808的人挑出来，看有多少学生？
均分=73.69
也就是选取：
低分数为：73.69-13.808*2=46.07-->46分
高分数为：73.69+13.808*2=101.30-->100分
在[46,100]分数范围的人我们就挑出来，看有多少人。

306/325=94.15%
3.三个标准差有多少人？

看实例：
标准差为13.808，我们把比均高三个13.808的人和比均分低三个13.808的人挑出来，看有多少学生？
均分=73.69
也就是选取：
低分数为：73.69-13.808*3=32.26-->32分
高分数为：73.69+13.808*3=115.11-->100分
在[32,100]分数范围的人我们就挑出来，看有多少人。

320/325=98.4615385%
三个不同标准差的对应人数范围：

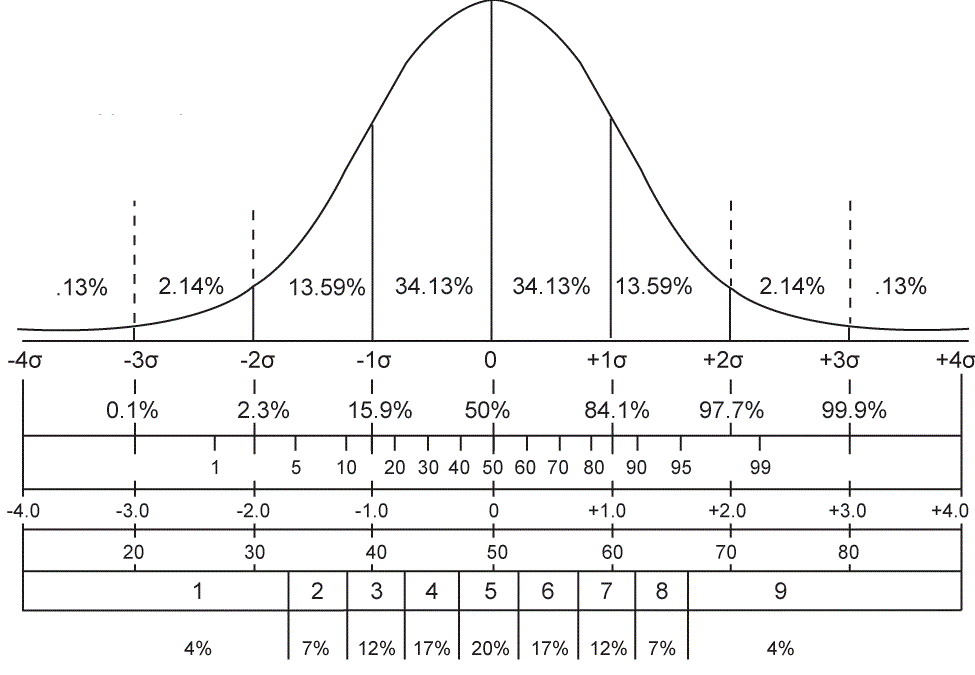
标准差	占比	Z值
一个标准差	68%	1
两个标准差	95%	1.96
三个标准差	99.7%	2.58

六、怎么预测分数
已经算出均分了，而且得到了标准差，就可以进行下一步操作了。
也就是说，可以用一定把握估计自己的学生在全部中的位置。如果有95%的把握说自己的学生跟别的学生（排除极个别差生现象-占5%）是一样的。那么就应该在一定的标准差范围内。
a=样本平均值-z*标准误差
b=样本平均值+z*标准误差
z就是上面的不同标准差的对应值。
本次测试：
均分：73.69
标准差：13.808
人数：325
可以算出人数开方：
325开方=18.02776
标准差与人数方的比：
13.808/18.02776=0.76593
95%把握情况下：
对应的Z是1.96
低分：
73.69-0.76593*1.96=72.18877714
高分：
73.69+0.76593*1.96=75.19122286
绕了一个大圈圈，其实人家都告诉了。

这就是问题。
七、有效性
其实这在大多数情况下，可能是正确的，但是一用就错，原因在于：很多时候，自己学生并不能代表大多数。
问题在于两极分化。

这种情况是常见的，但是又不能两眼一抹黑，不管了，那结果就是越教越差。
可以在前面乘以1.15-1.2的一个数 而且，65分的均分和76相比有较大差距，说明教学上要注意，注意考点教学，注意背诵，不要被拉更大距离，尽快提高分数。
八、正态分布
九、
附：数据下载
1.全市统考成绩2.全区统考成绩3.半期测试成绩